Дюрация Маколея

Что такое Дюрация Маколея (Macaulay Duration)

Дюрация Маколея – это взвешенный средний срок погашения денежных потоков от облигаций.

Вес каждого денежного потока определяется путем деления приведённой стоимости денежного потока на цену облигации.

Дюрация Маколея часто используется управляющими инвестиционными портфелями, которые используют стратегию иммунизации.

Дюрация Маколея рассчитывается следующим образом:

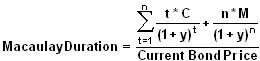
Где

t = соответствующий период времени.
C = периодическая купонная выплата.
y = периодическая доходность.
n = общее число периодов.
M = стоимость в срок погашения.
Текущая цена облигации = Текущая стоимость денежных потоков.

Итак, давайте разберёмся, что такое дюрация Маколея

Этот параметр назван в честь своего создателя, Фредерика Маколея. Дюрацию Маколея можно рассматривать как точку экономического баланса группы денежных потоков.

Согласно другому способу интерпретации статистики, это средневзвешенное количество лет, в течение которых инвестор должен поддерживать позицию по облигации, чтобы текущая стоимость денежных потоков по облигации оказалась равна сумме, уплаченной за облигацию.

Факторы, влияющие на дюрацию Маколея

Цена облигации, срок погашения, купонная выплата и доходность к сроку погашения – вот все факторы, которые используются при расчёте дюрации.

Если все остальные факторы равны, по мере увеличения срока погашения дюрация тоже увеличивается.

По мере увеличения купонной выплаты по облигации её дюрация уменьшается.

По мере увеличения процентных ставок дюрация уменьшается, и чувствительность облигации к дальнейшему повышению процентных ставок снижается.

Кроме того, наличие амортизационного фонда, график авансовых выплат до погашения и возможность досрочного погашения снижают дюрацию облигации.

Пример расчёта

Рассчитать дюрацию Маколея довольно просто.

Предположим, что у нас есть облигация с номинальной стоимостью в 1000$, по которой выплачивается купон 6%, а срок погашения наступает через три года.

Процентные ставки составляют 6% годовых с начислением раз в полгода. Купонные выплаты по облигации выплачиваются два раза в год, а основная сумма – при окончательном расчёте.

С учетом этого в течение следующих трёх лет ожидается поступление следующих денежных потоков

Период 1: 30$.
Период 2: 30$.
Период 3: 30$.
Период 4: 30$.
Период 5: 30$.
Период 6: 1030$.

Имея информацию о периодах и денежных потоках, мы можем рассчитать коэффициент дисконтирования для каждого периода.

Данный показатель рассчитывается по формуле 1 / (1 + r)n, где r – это процентная ставка, а n – это номер периода.

Процентная ставка (r), начисляемая раз в полгода, составляет 6%/2 = 3%.

Таким образом, коэффициенты дисконтирования будут выглядеть следующим образом

Коэффициент дисконтирования первого периода = 1 / (1 + 3%)1 = 0,9709.
Коэффициент дисконтирования второго периода = 1 / (1 + 3%)2 = 0,9426.
Коэффициент дисконтирования третьего периода = 1 / (1 + 3%)3 = 0,9151.
Коэффициент дисконтирования четвёртого периода = 1 / (1 + 3%)4 = 0,8885.
Коэффициент дисконтирования пятого периода = 1 / (1 + 3%)5 = 0,8626.
Коэффициент дисконтирования шестого периода = 1 / (1 + 3%)6 = 0,8375.

Теперь умножьте денежный поток периода на номер периода и соответствующий коэффициент дисконтирования, чтобы найти текущую стоимость денежного потока

Период 1 = 1 х 30$ х 0,9709 = 29,13$.
Период 2 = 2 х 30$ х 0,9426 = 56,56$.
Период 3 = 3 х 30$ х 0,9151 = 82,36$.
Период 4 = 4 х 30$ х 0,8885 = 106,62$.
Период 5 = 5 х 30$ х 0,8626 = 129,39$.
Период 6 = 6 х 1030$ х 0,8375 = 5175,65$.

Сумма этих значений = 5579,71$ = числитель (нумератор).

Текущая цена облигаций = сумма денежных потоков = 30/(1 + 3%)1 + 30/(1 + 3%)2 ++ 1030/(1 + 3%)6 = 1000$ = знаменатель (деноминатор).

(Обратите внимание, что, поскольку купонная и процентная ставка одинаковы, облигация будет торговаться по номиналу)

Дюрация Маколея = 5579,71$ / 1000$ = 5,58.

У облигации с купонными выплатами дюрация всегда будет меньше срока погашения.

В приведённом выше примере дюрация в 5,58 полугодия меньше, чем срок погашения в шесть полугодий. Другими словами, 5,58/2 = 2.79 года, что меньше трёх лет.

Связанные термины

Модифицированная дюрация (Modified Duration)

Модифицированная дюрация – это формула, выражающая измеримое изменение стоимости ценной бумаги в ответ на изменение процентных ставок.

Эффективная дюрация (Effective Duration)

Эффективная дюрация – это расчётное значение для облигаций со встроенными опционами в котором учитывается, что ожидаемые денежные потоки при изменении процентных ставок будут колебаться.

Облигация разового погашения (Bullet Bond)

Облигация разового погашения – это долговой инструмент, полная номинальная стоимость которого выплачивается одним разом в дату погашения.

Понятие чувствительности к процентным ставкам (Interest Rate Sensitivity)

Чувствительность к процентным ставкам – это показатель того, насколько сильно будет колебаться цена актива с фиксированным доходом в результате изменения процентной ставки.

Дюрация (Duration)

Значение дюрации показывает, сколько лет потребуется для получения истинной стоимости облигации, путём определения средневзвешенного значения текущей стоимости всех будущих купонных и основных выплат.